Happy New Year for those who celebrate!
Happy Arbitrarily Chosen Point in Earth's Orbit for those how don't!
We all know that the proper lighting factor (i.e. proportion of reflected incoming light) for a completely diffuse (aka Lambertian) surface is \(\max(0, L\cdot N)\). Here, \(L\) is the direction to the light source, \(N\) is the surface normal, and \(\cdot\) is the dot product. The dot product essentially comes from pure geometry (the same amount of light in a light beam cross-section being spread across larger surface area), while the \(\max\) is there to make sure that the parts of the surface facing away from light don't receive any light at all.
Is it a great, physically reasonable model (although real materials don't exactly look like that), and serves as a basis for many other shading models (typically via microfacet theory for modern PBR materials). However, sometimes we don't care about such things; sometimes we've just started a new project or a rendering tech demo and we just want to throw some good one-liner shading model. We don't have a texture or even don't intend to, we just want something reasonable to look at.
And here the diffuse model sucks! The \(\max(0, \dots)\) part makes half of the model (the one not facing the light) completely flat-colored (e.g. just black if you don't have ambient light), making you unable to see any geometry.

Notice the black parts!
Btw, all screenshots in this post have light intensity of 1, have gamma-correction, and no other post-processing (i.e. no tone-mapping).
Can we do better?
Contents
Typical solutions
Now, of course it's not a new problem. In typical scenes this effect isn't seen because we have many different lights (so the black part is much smaller), we have textures (so with some ambient light there is still variation in the color), we have some form of ambient occlusion (which further provides visual clues about the geometry), etc, etc.
All these solutions are, however, not one-liners like the max(0, dot(L, N)) thing, and range in complexity from rather simple (e.g. hard-coding two or three lights in the shader) to academic-level state-of-the-art (like GTAO and similar algorithms). For something like a test project we would definitely prefer a one-liner!
A silly solution
One simple way to fix this is to just re-map the dot product values from \([-1, 1]\) to \([0, 1]\) with a linear function. This results in a formula
\[ 0.5 + 0.5 \cdot (L\cdot N) = \frac{1 + L\cdot N}{2} \]Here's what it looks like:

It's much better, and there are no completely black spots, but the image is much brighter than it should be. It makes sense — after all, we changed the formula! Comparing the plots of intensity as a function of the dot product makes it especially apparent:
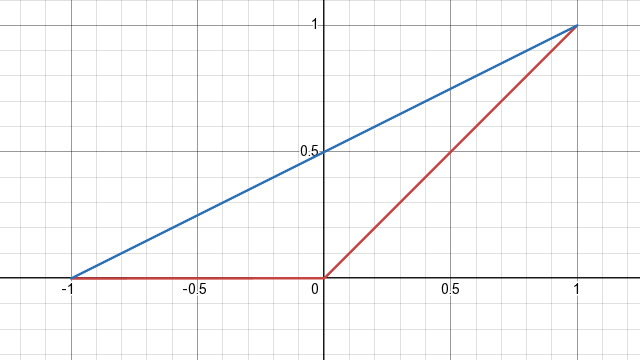
Red is correct formula, blue is tweaked formula
It's not exactly physical, but it probably can be put on rigorous grounds if we replace a single directional light source with a suitable environment map, e.g. one that has light in one hemisphere and doesn't have it in the other hemisphere (though I didn't check the math). That's what I've been doing for ages, but maybe we can do even better?
A sillier solution
Behold:
\[ \left(0.5 + 0.5 \cdot (L\cdot N)\right)^2 = \left(\frac{1 + L\cdot N}{2}\right)^2 \]Yep, I just squared the formula from the previous section! Here's what it looks like:

It's much closer to the true image in well-lit areas, yet still has nice shading gradients where the surface isn't facing the light. It's not exactly physical either, though we might hand-wavingly say that it approximates subsurface scattering of some sort. And here's the plot:
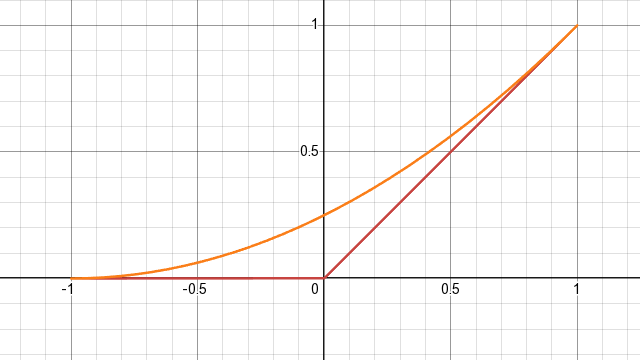
Red is correct formula, orange is new formula
It's clearly some sort of an approximation of the true formula! How come?
Hermite problems
If you look closely at the last plot above, you'll notice that
- Both functions have the same values at \(-1\) and \(1\)
- Both functions have the same slope (i.e. derivative) at \(-1\) and \(1\)
What if we turn things upside down and instead ask for a function that matches the values and derivatives of \(f(x) = \max(0, x)\) at \(x=\pm 1\)?
Guess what, mathematicians know exactly how to do this! This is called Hermite interpolation, and is solvable with an exact formula! If you specify \(N+1\) values and derivatives at various points, Hermite interpolation gives you the unique polynomial of order \(\leq N\) which has these values and derivatives.
In our case we have \(N=3\) (we have two values + two derivatives, thus \(N+1=4\)), so we expect at most a cubic polynomial. In this special case it turns out that the solution is not cubic, but quadratic, and is exactly \(\left(\frac{1+x}{2}\right)^2\). So this shading model is even optimal in some sense!
Hermite interpolation is also fun from algebraic perspective — it's actually an instance of the Chinese remainder theorem (for polynomial rings), which in modern form is neither Chinese nor about remainders.
That's it
I actually developed (well, more like randomly made up) this shading model while working on clouds in my game — they use exactly this formula, and I'm more than happy with how it looks:

That's it, and thanks for reading!