This post is much more math-y than my usual stuff. I just got this in my head for a while and decided to write it up. I even added MathJax to my blog for that!
When we think about inverses, we usually take uniqueness for granted. Like, 0.5 is the inverse of 2, and how can there be anything else?
However, the question of inverses is much more delicate when we work with something non-commutative, or worse, infinite-dimensional, as I'll show in this post.
Don't be scared of terminology; I explain everything we need as we go.
Let's start with simple stuff, though.
Contents
Numbers
Say, we're working with numbers. Rational numbers \(\mathbb Q\), real numbers \(\mathbb R\), complex numbers \(\mathbb C\), it doesn't really matter, as long as we can do arithmetics with them, including division (i.e. they form a field).
We have a number \(a\), and some number \(b\) is its inverse, meaning \(a\cdot b=1\). Let's say we have another number \(c\) which is also the inverse of \(a\), meaning \(a\cdot c=1\). Can it be that \(b \neq c\), i.e. \(a\) has two different inverses?
The answer is no, and the proof is two lines of school-level algebra: consider the number \(c\cdot a\cdot b\):
\[c\cdot a\cdot b = c\cdot (a\cdot b) = c \cdot 1 = c\] \[c\cdot a\cdot b = (c\cdot a)\cdot b = 1 \cdot b = b\]Since \(b\) and \(c\) are both equal to the same thing, they are just equal. QED.
Unfortunately, if you google "uniqueness of matrix inverse", you get a dozen posts with the very same proof. I'll show that this question is much deeper than that!
Non-commutative algebras
When talking about things that can be both added and multiplied (like numbers, polynomials, matrices, etc), "non-commutative" always refers to multiplication. Such structures (with addition & multiplication) are called algebras, and a non-commutative algebra is one where it happens that \(a\cdot b \neq b\cdot a\).
It makes a lot of sense if we think of elements of our algebra as some operations or processes: many things work differently when combined in different orders! Say, I paint my wall in black, and then I paint it in yellow, or vice versa – the result clearly depends on the order of these actions. Or maybe I sit on my wooden chair, and then break it into pieces with an axe. Try doing that in a different order! You get the idea.
This is exactly the reason why the matrix algebra is non-commutative: matrices represent linear transformations of vectors, i.e. some operations on vectors, and matrix multiplication is composition of these operations, and the result depends on the order of composition. The classical example is composing rotation and translation:
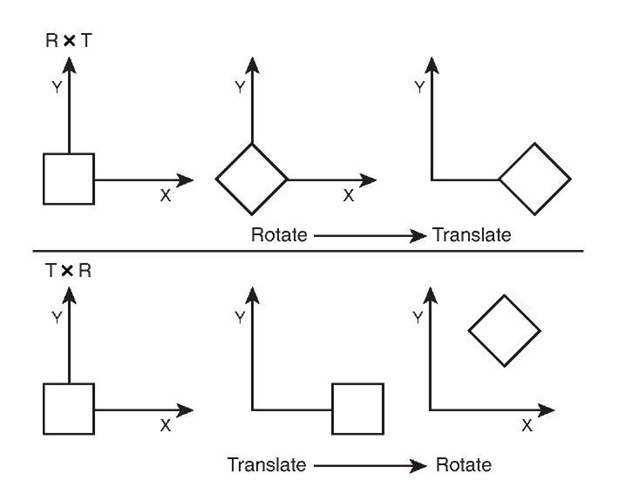
Of course, you'll need homogeneous coordinates to represent translations as matrices, which is common in e.g. 3D graphics.
In fact, starting with 3 dimensions, rotations only are already non-commutative.
Non-commutative inverses
So, non-commutativity is natural and expected, but also a huge pain. What does an inverse even mean in this case?
If we have two elements \(a\) and \(b\) such that \(a\cdot b=1\), do we say that they are inverses of each other? Well, that wouldn't be a good idea in general, because we know nothing about \(b\cdot a\)! We didn't have this problem with numbers because numbers were commutative: \(a\cdot b = b\cdot a\).
In the non-commutative case we talk about left inverses and right inverses separately. If \(a\cdot b=1\), we say that \(a\) is a left inverse of \(b\), and \(b\) is a right inverse of \(a\).
So, what about their uniqueness? Suppose that an element \(a\) has two right inverses: \(a\cdot b=1\) and \(a\cdot c=1\). Let's try repeating the proof above:
\[c\cdot a\cdot b = c\cdot (a\cdot b) = c \cdot 1 = c\] \[c\cdot a\cdot b = (\color{red}{c\cdot a})\cdot b = (\color{red}{???}) \cdot b = \color{red}{???}\]The proof doesn't work: it wants \(c\cdot a\), but we only know that \(a\cdot c = 1\)!
However, you might have noticed that if \(c\) is a left inverse of \(a\), i.e. if \(c\cdot a=1\), the proof works without any changes! I'll repeat this in full: if an element \(a\) has a right inverse \(b\) and a left inverse \(c\), then they are equal: \(b = c\).
So, any two different-sided inverses (i.e. one left and one right) are equal. In this case, if an element has many right inverses and at least one left inverse, all these right inverses are equal to this left inverse, and so they are equal to each other. In other words, if an element has at least one left inverse and at least one right inverse, all its inverses are equal, i.e. it has a unique inverse!
So, can it happen that an element has e.g. left inverses but no right inverse? Oh yes it can.
Infinite-dimensional algebras
Sounds cool already, huh?
Let's talk about infinite sequences of real numbers (or any other numbers, it doesn't matter). These are of the form \((x_0, x_1, x_2, \dots)\). They form a vector space: you can add them (component-wise), you can multiply them by a number (multiply all coordinates by the number), etc.
If they are a vector space, there are linear operators on this space. Something like a matrix, but with an infinite number of entries. To be honest, it is a bit hard to think about these operators in terms of infinite matrices, and a simpler point of view is just to think what every operator does to the input sequence.
Consider the right-shift operator \(R\): it shifts the sequence to the right, and appends a zero at the beginning:
\[ R(x_0, x_1, \dots) = (0, x_0, x_1, \dots) \]Similarily, a
left-shift operator
\(L\) shifts the sequence to the left, dropping the first term: \[ L(x_0, x_1, x_2, \dots) = (x_1, x_2, \dots) \]What happens if we multiply this operators? Remember, multiplication and composition are the same for linear operators (by definition):
\[ (L\cdot R) (x_0, x_1, x_2, \dots) = L(R(x_0, x_1, x_2, \dots)) = L(0, x_0, x_1, x_2, \dots) = (x_0, x_1, x_2, \dots) \] \[ (R\cdot L) (x_0, x_1, x_2, \dots) = R(L(x_0, x_1, x_2, \dots)) = R(x_1, x_2, \dots) = (0, x_1, x_2, \dots) \]So, \(L\cdot R\) doesn't change the input sequence, meaning \(L \cdot R=1\) (here, \(1\) is the identity operator), but \(R\cdot L\) replaces the first element of the sequence with zero, so \(R\cdot L\color{red}{\neq}1\). \(L\) is a left inverse of \(R\), and \(R\) is a right inverse of \(L\), but not the other way round.
This means that \(L\) doesn't have a left inverse at all, – otherwise, it would be equal to the right inverse, which is \(R\), so \(R\) would be a left inverse of \(L\), which would mean \(R\cdot L = 1\), which we know is false. Similarly, \(R\) doesn't have a right inverse.
In fact, if we define a family of operators \( R_s(x_0, x_1, \dots) = (s\cdot x_0, x_0, x_1, \dots) \) that do a right shift and append a copy of \(x_0\) multiplied by a fixed number \(s\) instead of zero, and all of them are right inverses of \(L\):
\[ (L\cdot R_s) (x_0, x_1, x_2, \dots) = L(R_s(x_0, x_1, x_2, \dots)) = \\ = L(s \cdot x_0, x_0, x_1, x_2, \dots) = (x_0, x_1, x_2, \dots) \]So \(L\cdot R_s = 1\), meaning \(L\) has many different right inverses, which can only happen if it doesn't have a left inverse.
Spooky stuff, if you ask me.
Matrices
This doesn't happen to matrices, though. At least not in finite dimensions (whether or not to even call infinite-dimensional beasts matrices is a separate question).
A usual proof that matrices have two-sided inverses usually explicitly computes the inverse anyway:
\[ A^{-1} = \frac{1}{\det A}\operatorname{adj}A \]where \(\det A\) is the determinant, and \( \operatorname{adj}A \) is the adjugate of the matrix \(A\), formed by replacing each element with the determinant of the whole matrix without the current row and column (called the cofactor matrix), and taking the transpose.
Quite a lot of determinants involved. Needless to say, any computations with this monstrosity are terrifying.
However, we can prove that matrix inverses are unique without computing said inverses at all! In fact, this isn't special to matrices: this works in any finite-dimensional algebra (or, more generally, any Artinian ring).
Finite-dimensional algebras
Any algebra is a vector space, so we can speak of its dimension. The algebra \(M_N\) of \(N\times N\) matrices has dimension \(N^2\). The algebra of complex numbers \(\mathbb C\) has dimension 2 if the base scalar field is the real numbers \(\mathbb R\). The algebra of real polynomials in one variable \(\mathbb R[X]\) is infinite-dimensional. The Clifford algebra \(\operatorname{Cl}(\mathbb R^N)\) of an N-dimensional Euclidean space has dimension \(2^N\).
Finite-dimensional algebras are quite special, because we can often deduce some properties of them just by using the dimensions. This is exactly what I'm going to do with inverses.
I want to prove the following: in a finite-dimensional algebra \(\mathbb A\), if some element \(a\) is a left inverse of element \(b\), then \(a\) also is a right inverse for some element \(c\). In other words, if \(a\cdot b=1\), then \(c\cdot a=1\) for some element \(c\). From that it will follow, combining with all our previous discussions, that \(b=c\) and inverses are unique in this algebra.
Left ideals
To prove this, we will consider the sequence of sets \(I_n = \{x\cdot a^n, x \in \mathbb A\}\). These are called principal left ideals generated by powers of \(a\). We don't need the full definition of a left ideal here, although it isn't much complicated. Also note that \(I_0 = \mathbb A\), which isn't relevant to us but still funny.
Two things are special about this sequence. First of all, each \(I_n\) is not just a subset of our algebra \(\mathbb A\), but a vector subspace. This is because \(I_n\) is closed under addition and multiplication by a scalar:
\[ x\cdot a^n + y\cdot a^n = (x+y)\cdot a^n \in I_n \] \[ \lambda \cdot (x\cdot a^n) = (\lambda\cdot x)\cdot a^n \in I_n \]As such, it has a dimension, which is necessarily finite (because the whole algebra has finite dimension).
Secondly, this sequence is a descending chain, meaning each set is contained in the previous one \(I_{n+1} \subseteq I_n\). This is easy to show as well:
\[ I_{n+1} \ni x\cdot a^{n+1} = x\cdot (a \cdot a^n) = (x\cdot a)\cdot a^n \in I_n \]The secret ingredient
So, we have a sequence of vector subspaces of our algebra, and each subspace is contained in the previous one, which means its dimension is less or equal to the dimension of the previous one \(\dim I_{n+1} \leq \dim I_n\). In other words, the sequence of dimensions \((\dim I_n)\) is non-increasing.
A non-increasing sequence of natural numbers (dimensions cannot be negative or fractional, not for vector spaces) is quite special: it cannot be always decreasing. I.e. it cannot happen that \(\dim I_0 > \dim I_1 > \dim I_2 > \dots\) and so on, with all inequalities being strict. If, for example, \(\dim I_0 = 4\), we could have a sequence \(4 > 3 > 2 > 1 > 0\) and now we cannot continue because there is no natural number less than zero! This is basically the property of natural numbers being well-ordered, the same property that enables induction.
So, the sequence of dimensions is non-increasing, but is also cannot be always decreasing. What this means is that at some point this sequence of dimensions has two equal consecutive elements, meaning \(\dim I_{n+1} = \dim I_n\) for some \(n\). This is the secret ingredient of the proof, the key observation which requires the algebra to be finite-dimensional.
Final proof
So, \(\dim I_{n+1} = \dim I_n\), and these are vector spaces, and one contains the other. This means that they are simply equal: \(I_{n+1} = I_n\).
Now, \(I_n\) contains elements of the form \(x\cdot a^n\). Taking \(x=1\) we see that it contains \(a^n\). Since \(I_{n+1} = I_n\), \(I_{n+1}\) also contains \(a^n\).
Elements of \(I_{n+1}\) are of the form \(x \cdot a^{n+1}\), and \(I_{n+1}\) contains \(a^n\), which means it is also of this form \(c \cdot a^{n+1} = a^n\).
Remember that \(a\) has a right inverse \(b\), meaning that \(a\cdot b=1\). Let's multiply the equation \(c \cdot a^{n+1} = a^n\) by \(b\) on the right \(n\) times (or, equivalently, multiply by \(b^n\)):
\[ \begin{align}c \cdot a^{n+1} \color{blue}{\cdot b} = a^n \color{blue}{\cdot b} &\Longrightarrow c \cdot a^n = a^{n-1} \\\ c \cdot a^n \color{blue}{\cdot b} = a^{n-1} \color{blue}{\cdot b} &\Longrightarrow c \cdot a^{n-1} = a^{n-2} \\\ &\dots \\\ c \cdot a^2\color{blue}{\cdot b} = a \color{blue}{\cdot b} &\Longrightarrow \color{blue}{c \cdot a = 1} \end{align} \]So, \(c\cdot a = 1\), meaning \(a\) has a left inverse. It also has a right inverse \(b\), which means \(b=c\) and all (left and right) inverses of \(a\) are equal, meaning it has a unique inverse. Hooray!
The argument applies to any finite-dimensional algebra. If you're working with Clifford algebras (also known as geometric algebra), inverses are unique there, too, and left inverses are automatically right inverses and vice versa. This should simplify some equations, I guess :)
Mmm...yeah, that's it!
I don't think I'll stop writing on math topics anytime soon; I have at least a couple of other pure-math posts hatching in my head.
As always, thanks for reading!