A simple texture atlas packing algorithm

2022 Aug 6

The problem

Recently I was adding shadow mapping support to the martian-droid-colony-building project I'm working on, and I wanted to support pretty much arbitrary number of shadows (neglecting the performance implications), so the main question is: how do I access the shadow maps in the shader?

I use OpenGL 3.3, so I don't have that many options:

Use a separate texture per shadow map, and an array of samplers in the shader

There is a limit to the possible number of samplers per shader stage (which is something like 16 at minimum), so I'll be severely constrained in the number of simultaneous shadows
I'd need a separate framebuffer for each shadow map, and switching framebuffers aint cheap

Use an array texture

The limits are much more forgiving (at least 256 array texture layers for OpenGL 3.3)
All shadow maps are forced to have the same size (and I'd really want to give less precision to shadows from far away lights)
The framebuffer issue is also present (you can only attach a single layer of an array texture to a framebuffer)

Use a texture atlas, i.e. a single texture with all shadow maps side by side

No limits on the number & sizes of the textures (apart from the limits on the atlas size itself)
A single framebuffer is sufficient for rendering into it

So, I settled on the texture atlas approach. It looks roughly like this:

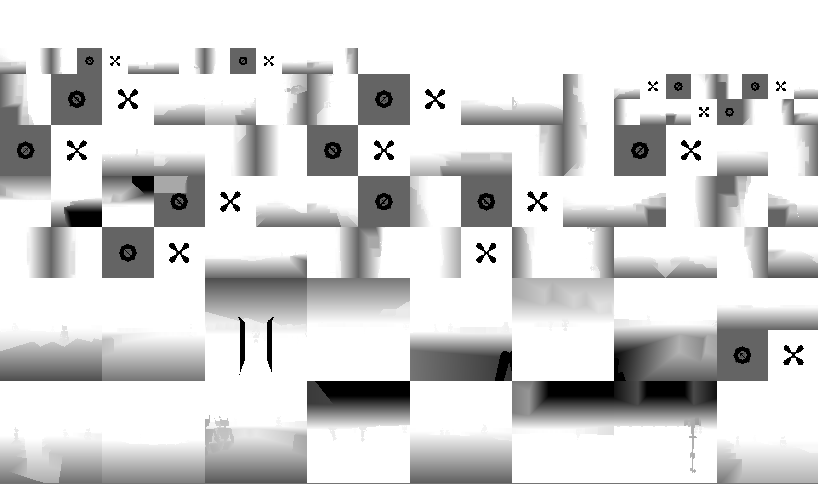
It contains a single shadow map for each spot light, and 6 shadow maps for each point light (an unfolded cubemap). I tried dual paraboloid shadow maps for point light sources, but the paraboloid projection produced too much distortion for my geometry:

Now the problem is: how exactly am I going to pack different shadow maps with different sizes into a single texture? In general, the 2D packing problem is a pretty complicated one, with most solutions being either too slow or far from optimal (see here and here for an overview of existing solutions). However, my problem at hand is hardly general, and I can afford a few hugely simplifying assumptions:

Textures are always square (makes sense both for spot light shadows, which must cover a circular area, and for point light shadows, which are faces of a cube)
Textures always have size 2^k
The destination atlas has size 2ⁿ
The total area of all the textures doesn't exceed the area of the atlas

Note that it is easy to enforce the last assumption by pre-computing the total area of all the shadow maps and comparing it to the area of the atlas: if they don't fit, simply scale all shadow maps down by a factor of 2 (which scales the total area down by 4) until they fit. Alternatively, remove shadow maps (e.g. for lights that are too far away) until the remaining shadow maps fit.

I also assume that we don't want the packed textures to persist, i.e. reuse them between frames (and e.g. render each shadow map once every several frames), so that the position and size of the shadow maps for a particular light source can change every frame.

The solution

After a bit of thinking, I came up with a very simple algorithm that solves the problem. The idea of the algorithm is:

Start from the largest textures and pack them, then the second largest, and so on up to the smallest ones
For the largest textures of size 2^k×2^k, we subdivide the atlas into 2^n-k×2^n-k cells of size 2^k; since the total area of all textures is less than the area of the atlas (property 4 above), we are guaranteed that the number of textures of this size is no larger than the number of cells. So, simply allocate one cell per each texture of size 2^k×2^k
We are left with some cells of size 2^k×2^k and the next texture size is 2^m×2^m with m < k; split every 2^k×2^k cell into 2^k-m×2^k-m cells of size 2^m×2^m; again, we know that the number of textures is no larger than the number of cells, so allocate on per each texture;
Recursively do the same with all texture sizes.

The assumption that all texture sizes are powers of two allows us to use this cell subdivision idea and guarantees that we always can fit the textures into the atlas. However, the naive approach of storing all the cells and explicitly subdividing them is too expensive, and there's a much simpler way!

Notice that it really doesn't matter which cells we allocate for which texture (we could even do this randomly!), so we can select some simple to implement allocation rule. On such rule is: always allocate the leftmost cell from the topmost not-completely-filled row of cells. This means that, at any point of the algorithm, the filled cells look like a ladder descending from left to right:

So, to track the availability of particular cells, we only need to track the corners of this ladder! These corners (red dots in the picture above) always correspond to the bottom-right corners of some allocated textures. Storing them in the order of their X-coordinate, we get the following outline of the algorithm:

Initialize the current pen position to (0,0)
Sort the texture sizes in descending order
For each texture of size S (which is a power of 2):

Allocate the region [pen.x, pen.x + S] x [pen.y, pen.y + S] for this texture
Offset the pen position: pen.x += S
Update the ladder data:

If the ladder is empty, insert the corner (pen.x, pen.y + S)
Otherwise, if the last corner in the ladder has Y-coordinate larger than pen.Y + S, insert the corner (pen.x, pen.y + S)
Otherwise (i.e. the ladder is not empty and it's last corner has its Y-coordinate coinciding with the new corner we just created by allocating the texture), move the last corner's X-coordinate to pen.x

If we reached the right end of the atlas, i.e. if pen.x == atlas_width:

Remove the last element from the ladder (it corresponds to the corner that hit the right edge of the atlas)
Update the pen Y-coordinate: pen.y += S
Update the pen X-coordinate:

If the ladder is nonempty, set pen.x = ladder.back().x
Otherwise, there are no corners, so we can start from the left edge: pen.x = 0

This looks a bit overwhelming, but is actually rather intuitive after you've traced all the steps. Here's a standalone C++ implementation:

struct point
{
    int x, y;
};

struct box
{
    point topleft;
    point bottomright;
};

std::vector allocate_texture_atlas(
    point const & atlas_size,
    std::vector const & texture_sizes)
{
    // we have to separately sort the indices so that the i-th region
    // of the output corresponds to the i-th texture size of the input
    std::vector sorted(texture_sizes.size());
    for (int i = 0; i < sorted.size(); ++i)
        sorted[i] = i;

    // sort in descending order
    std::sort(sorted.begin(), sorted.end(), [&](int i, int j){
        return texture_sizes[i] > texture_sizes[j];
    });

    std::vector ladder;

    point pen{0, 0};

    std::vector result(texture_sizes.size());

    for (int i : sorted)
    {
        int const size = texture_sizes[i];

        // allocate a texture region
        result[i] = {{pen.x, pen.y}, {pen.x + size, pen.y + size}};

        // shift the pen to the right
        pen.x += size;

        // update the ladder
        if (!ladder.empty() && ladder.back().y == pen.y + size)
            ladder.back().x = pen.x;
        else
            ladder.push_back({pen.x, pen.y + size});

        if (pen.x == atlas_size.x)
        {
            // the pen hit the right edge of the atlas
            ladder.pop_back();

            pen.y += size;
            if (!ladder.empty())
                pen.x = ladder.back().x;
            else
                pen.x = 0;
        }
    }

    return result;
}

It produces atlases like these:

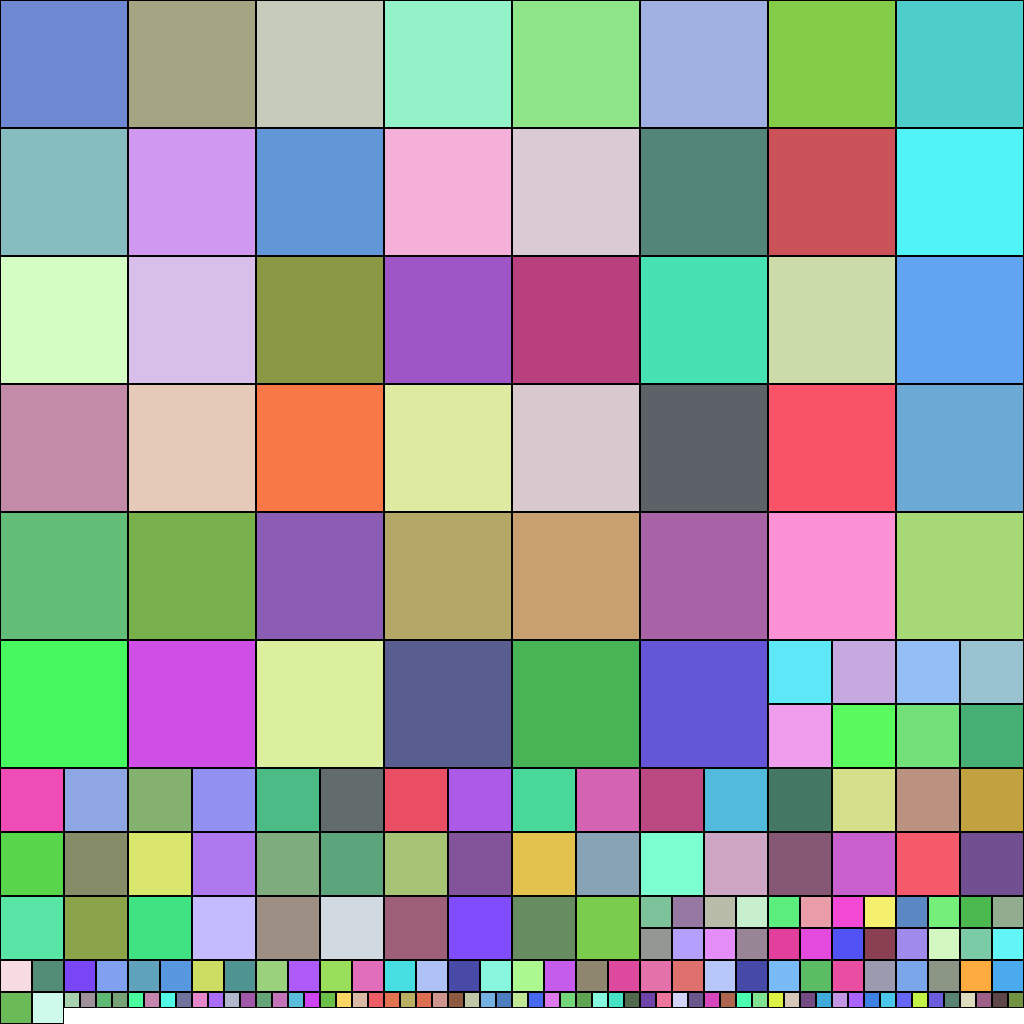
The algorithm has \( O(n \cdot \log n) \) complexity due to sorting; everything after sorting is \( O(n) \). We could further optimize the algorithm in several ways:

Remove the allocation of sorted array by sorting the original texture_sizes array in-place; you'll want to store light indices together with texture sizes (e.g. something like vector<pair<light_index, texture_size>>, otherwise you won't know which allocated regions correspond to which textures after sorting (this is why my implementation sorts the texture indices, not the sizes themselves)
Use a fixed-sized array instead of a vector for the ladder: it never contains two corners corresponding to textures of different sizes, so for an atlas of size 2ⁿ you can never have more than n elements in the ladder array
Use counting sort: we know that the texture_sizes array contains only a handful of specific numbers (that is, powers of two), so we can instead have something like a vector<vector<int>> or vector<int>[N] such that the k-th vector stores the indices of all textures that have size 2^k, descreasing the overall algorithm complexity to the sweet \( O(n) \). Now that I think of it, I probably should actually do this in my implementation...

So, that's it! Take the algorithm with a grain of salt: I have only tried it, not proved it is correct. Anyway, hope this helps, and thanks for reading!

Contents

The problem

The solution