(Yet another) Introduction to quaternions

2024 Oct 26

There are thousands of articles about quaternions on the internet, but my social media said it won't hurt to have another one, so pretend you know nothing about quaternions, and let's roll.

Some people said that the biggest problem of all articles on quaternions is the abundance of formulas. Honestly, I have no idea how you could explain a mathematical object without formulas, though I will try to make them as innocent as possible. There will be a lot of algebra (but mostly very basic algebra), which we can't escape – quaternions are an algebraic object, after all. I'll try to derive all formulas except for a couple that are exceptionally long and boring.

Finally, a word about "understanding" quaternions. As von Neumann said, in maths you don't understand things, you just get used to them, and I tend to agree. With enough practice and exposure, you gradually become familiar with the subject and develop an internal intuition for it. When this happens repeatedly, at some point you say that you understand it. It might seem that a particular article, or book, or video made you finally understand, while in reality you probably already almost understood everything, and this last article just filled up one last bit of interwoven connections that you somehow missed, which made everything finally click and make sense.

Contents

Motivation: 3D rotations

Say, you're making a 3D game, and you need to work with rotating objects. Rotations are certain 3D transformations; it turns that they are always linear transformations, and can be expressed using a \(3\times 3\) matrix. Not every matrix represents a rotation, though; in fact, rotation matrices form a certain very special type of matrices. When you see such a matrix, say

\[ \begin{pmatrix} 0.3978105 & -0.3063282 & -0.8648179 \\ 0.2806342 & 0.9380625 & -0.2031824 \\ 0.8734937 & -0.1618693 & 0.4591372 \end{pmatrix} \]

can you easily visualize what this rotation does? I'd be impressed if you can, because I can't! What's more, a rotation matrix takes up 9 floating-point values (so, 36 bytes for 32-bit floating point), while it is known that rotations only require 3 values (12 bytes) to be uniquely determined (using, for example, Euler angles), so we're using 3 times more memory then we would in a perfect world.

Why not use Euler angles, then? Well, it turns out they're even worse. A single Euler rotation is easy to visualize, e.g. a rotation of \(30^\circ\) around the X axis. But when you combine several such rotations around different axes (e.g. X, then Y, then Z), it's very hard to figure out what the resulting rotation is. Combining two rotations represented by two different triples of Euler angles is even worse. Not to mention than there are something like 24 or 48 different conventions about what exactly Euler angles mean and what they represent. Also they suffer from problems like gimbal lock, etc, etc.

Combining two rotations represented with matrices is dead easy: it is just matrix multiplication (or is it called AI these days?).

So, matrices use too much space, and are hard to reason about, but compose nicely. Euler angles save up on space, but are worse in pretty much any other way. Can we do better?

Motivation: 3D complex numbers

You probably know about complex numbers: they are formal sums of the form \(a+bi\) where \(a,b\in\mathbb R\) are usual real numbers, and \(i^2=-1\) is the magical sauce ingredient called the imaginary unit that makes complex numbers really cool. These have been known roughly from the 16'th century, and it took another 3 centuries for mathematicians to stop freaking out about them, but by the end of 19'th century they were already a routine mathematical object. Many people looked for some generalizations of complex numbers, say, containing not one, but two imaginary units, but it never worked out: the resulting systems of "numbers" always lacked some of the nice properties of complex numbers (not closed under multiplication, not all elements are invertible, stuff like that).

At least until Hamilton figured out that you need not two, but three imaginary units. Then everything just works, and you get a really cool and immensely important mathematical object. You do lose one thing, though: multiplication is no longer commutative, i.e. it isn't always true that \(a\cdot b=b\cdot a\). Later it was proved by Frobenius that, indeed, there isn't an analogue with two imaginary units, or any other number of them.

It also turned out that the very same mathematical object solves the previous problem of representing rotations! Is it a coincidence, or is it a natural consequence of some beautiful mathematics? Thing is, I don't know how to answer this question. It definitely isn't purely a coincidence, but it still looks rather miraculous.

That there is some nice algebra that is able to represent 3D rotations follows directly from the general framework of Clifford algebras, and imaginary units arise quite naturally there. However, nothing forces every non-zero element of this algebra to be invertible, and in fact this isn't true for split-biquaternions, the analogue used for 4D rotations. That regular quaternions are so nice seems to be a special feature that only exists in low \((<4)\) dimensions.

Behold: quaternions!

You've probably guessed that quaternions are exactly the answer to the questions from the previous two sections. The set of quaternions is usually denoted as \(\mathbb H\), in honour of Rowan Hamilton who figured them out. Before we dive into how they answer these questions, though, we need to figure out what quaternions really are.

Now, there are many equivalent ways to define quaternions:

Probably the simplest way to put this is to say that quaternions are just 4-dimensional vectors with real coordinates, together with some special multiplication rule. So, quaternions are 4-tuples of real numbers \((a,b,c,d)\), which we can add and subtract component-wise \[ (a,b,c,d)\pm(w,x,y,z) = (a\pm w,b\pm x,c\pm y,d\pm z) \] and also a multiplication of such tuples is defined:

\[ (a,b,c,d) \cdot (w,x,y,z) = (e,f,g,h) \]

where \((e,f,g,h)\) somehow depend on \((a,b,c,d)\) and \((w,x,y,z)\). We'll discuss the exact multiplication rule in just a minute. What is important is that it isn't commutative – in general, the result of multiplication depends on the order of the operands:

\[ p\cdot q \, {\color{red}\neq} \, q\cdot p \]

for arbitrary quaternions \(p\) and \(q\). This is to be expected, since 3D rotations don't commute either: the result of applying two rotations depends on the order of rotations.

Note that vectors can always be multiplied (scaled) by scalars, i.e. real numbers, and this operation is separate from quaternion multiplication. That is, given a quaternion \((a,b,c,d)\) and a real number \(k\), we can form the scalar-vector product

\[ k\cdot(a,b,c,d) = (ka,kb,kc,kd) \]

As we'll see shortly, there's actually no need to distinguish between these two types of product, as scalar-quaternion (i.e. scalar-vector) product is a special case of quaternion-quaternion product.

Some quaternions have special names; specifically

\[ i = (0,1,0,0) \\ j = (0,0,1,0) \\ k = (0,0,0,1) \]

These are the analogues of the imaginary unit in complex numbers. As we'll see shortly, their square is \(-1\).

We know that the 4-dimensional space of tuples of 4 numbers has a basis of 4 vectors; \(i,j,k\) are three vectors of this basis, but we've omitted the last one: \((1,0,0,0)\). Does it have a special name?

Now, this might look stupidly confusing, but it does have a special name: it is called \(1\). Yeah, I'm not joking, the quaternion \((1,0,0,0)\) is simply called \(1\). Why? Because it behaves exactly like the usual real number \(1\). In general, quaternions of the form \((a,0,0,0)\) behave exactly like the real number \(a\). We'll make this more precise a bit later. For the time being, I'll call this quaternion \(\mathbb I=(1,0,0,0)\) to avoid confusion between real numbers and quaternions.

By the usual rules of vector maths, any quaternion can be decomposed as a sum of basis quaternions with some real coefficients (that's the definition of a basis):

\[ (a,b,c,d) = a\cdot(1,0,0,0) + b\cdot(0,1,0,0) + c\cdot(0,0,1,0) + d\cdot(0,0,0,1) =\\ = a\mathbb I + bi + cj + dk \]

And since, as we've said, \(\mathbb I\) behaves exactly like the real number \(1\), this is often written as

\[ a\mathbb I + bi + cj + dk = a + bi + cj + dk \]

i.e. omitting \(\mathbb I\) altogether, and identifying it with the number \(1\). So, the notation \(a+bi+cj+dk\) really just means the quaternion \((a,b,c,d)\).

Quaternion multiplication

Now, the rule for multiplying quaternions is

\[ (a,b,c,d) \cdot (w,x,y,z) = \\ = (aw - bx - cy - dz, \\ ax + bw + cz - dy, \\ ay - bz + cw + dx, \\ az + by - cx + dw) \]

This might seem suspiciously arbitrary, but this rule is actually a consequence of a few simpler rules.

First of all, in algebra any multiplication must always be linear, i.e. distributive over addition:

\[ p\cdot(q+s) = p\cdot q + p\cdot s \\ (q+s)\cdot p = q\cdot p + s\cdot p \]

(Note that we have to state two separate rules, because we don't assume that multiplication is commutative). Here, \(p,q,s\) are some quaternions, and \(+\) is addition of quaternions (i.e. addition of 4-dimensional vectors).

It also has to commute with scalar multiplication, i.e. when encountering a product of quaternions and scalars, we can move the scalar around and the result won't change:

\[ s\cdot(q\cdot p) = (s\cdot q)\cdot p = q\cdot (s\cdot p) \]

Here, \(p\) and \(q\) are quaternions and \(s\) is a real number. This might sound obvious, but it's actually an extremely important rule that doesn't follow from other rules. (For example, it doesn't hold if we take complex numbers as our scalars, and think of quaternions as pairs of complex numbers; that is, \(\mathbb H\) is an \(\mathbb R\)-algebra, but not a \(\mathbb C\)-algebra).

Using this linearity rules, we can already somewhat simplify a product of two generic quaternions if we represent them as a sum of basis quaternions:

\[ (a,b,c,d)\cdot(w,x,y,z) = (a\mathbb I+bi+cj+dk) \cdot (w\mathbb I+xi+yj+zk) = \\ = aw\cdot \mathbb I^2 + bx\cdot i^2 + cy\cdot j^2 + dz\cdot k^2 + \\ + ax\cdot \mathbb I i + bw\cdot i\mathbb I + cz\cdot jk + dy\cdot kj + \\ + ay\cdot \mathbb I j + bz\cdot ik + cw\cdot j\mathbb I + dx\cdot ki + \\ + az\cdot \mathbb I k + by\cdot ij + cx\cdot ji + dw\cdot k\mathbb I \]

This might look even more intimidating and confusing than the original formula, but notice that here half of the products are just products of real numbers like \(aw\) or \(dx\) (btw here \(dx\) is not a differential or anything like that, it's just \(d\) multiplied by \(x\)), while the other half are products of basis quaternions like \(i^2\) or \(\mathbb I j\). But we already know how to multiply numbers, so the only thing we need to do is decide on how to multiply basis quaternions, of which there are only \(4\times 4=16\) different products. So, we've reduced the multiplication of two arbitrary quaternions to just 16 products of specific quaternions!

The next rule we need is about \(\mathbb I\): as I've said, it behaves exactly like a real number \(1\). But \(1\) multiplied with anything doesn't change that anything, i.e. \(1\cdot p=p\) is always true, no matter what exactly you mean by \(\cdot\) and \(p\). So, we arrive at the following multiplication rules:

\[ \mathbb I^2 = \mathbb I \\ \mathbb I\cdot i = i\cdot\mathbb I = i \\ \mathbb I\cdot j = j\cdot\mathbb I = j \\ \mathbb I\cdot k = k\cdot\mathbb I = k \]

which already settles 7 out of 16 multiplications we need to figure out! From here, we can see that quaternions of the form \(a\mathbb I = (a,0,0,0)\) behave like real numbers in disguise, i.e. their product is just the product of coefficients:

\[ (a,0,0,0)\cdot(b,0,0,0) = (a\mathbb I)\cdot(b\mathbb I) = ab\cdot\mathbb I^2 = ab\cdot\mathbb I = (ab,0,0,0) \]

and multiplying such a quaternion by an arbitrary quaternion is the same as multiplying it with a number \(a\):

\[ (a,0,0,0)\cdot(w,x,y,z)=(a\mathbb I)\cdot(w\mathbb I+xi+yj+zk)=aw\cdot\mathbb I^2 + ax\cdot\mathbb I i + ay\cdot\mathbb I j + az\cdot\mathbb I k = \\ = aw\cdot\mathbb I + ax\cdot i + ay\cdot j + az\cdot k = (aw,ax,ay,az) = a\cdot(w,x,y,z) \]

which is why we don't distinguish between scalar-quaternion and quaternion-quaternion multiplications.

From now on, I'll drop the \(\mathbb I\), and I'll simply write \(a+bi+cj+dz\) or something like that.

In algebra, instead of saying that \(\mathbb I\) behaves like \(1\), we usually simply say that the scalars embed into our algebra, i.e. that the quaternions literally contain the real numbers. These two points of view are completely equivalent, but I believe that, from a pedagogical point of view, it's nice to distinguish between numbers and quaternions, at least when just learning about them.

So, we're left with 9 basis quaternion multiplications for all possible combinations of \(i,j,k\). Here, the rules are

\[ i^2=j^2=k^2=-1\\ ij=-ji=k \\ jk=-kj=i\\ ki=-ik=j \]

These rules are what is usually called the multiplication table of quaternions, assuming that the other rules (lineariry and \(\mathbb I\) behaving like \(1\)) are implied (they are indeed always assumed in algebra, but it might not be obvious if you didn't spend several years studying algebra!).

This multiplication table is relatively easy to remember, actually:

Wikipedia features a graph showing all these relations, which for me looks like it makes things even more obscure, but who knows, maybe it'll work for you:

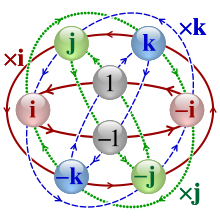
That completes our 9 remaining rules to get the total of \(7+9=16\) rules for products of basis quaternions \(\mathbb I,i,j,k\). If we insert these new rules into the full multiplication formula above, we get

\[ (a+bi+cj+dk) \cdot (w+xi+yj+zk) = \\ = (aw - bx - cy - dz) + \\ + (ax + bw + cz - dy)i + \\ + (ay - bz + cw + dx)j + \\ + (az + by - cx + dw)k \]

which is again a long and boring formula which is rather hard to remember directly. Thankfully, there's no need to remember it, as we'll see later.

You might ask: why exactly these multiplication rules? Linearity and \(\mathbb I\) being \(1\) kind of make sense, since without them it's really hard to do any computations with quaternions. However, the rules for \(i,j,k\) seem arbitrary. Why not e.g. say that \(i^2=j^2=1\) and \(k^2=-1\)? Well, it will be a different product, with different properties. In fact, it will be isomorphic to (\(\approx\) behaves in the same way as) the usual \(2\times 2\) matrices! (This fact is far from obvious, by the way!) What about \(i^2=j^2=-1\) and \(k^2=1\)? This will also be isomorphic to \(2\times 2\) matrices!

What about \(i^2=j^2=k^2=1\)? This will contradict other rules:

\[ 1 = i^2j^2 = i(ij)j = -i(ji)j = -(ij)(ij) = -k^2 = -1 \]

and from \(1=-1\) you can deduce that \(x=0\) for any \(x\). Thus, some multiplication rules even lead to contradictions! Jeez.

So, again, why these multiplication rules specifically? Well, because they lead to a particularly nice algebraic structure with useful properties, while other rules don't. It's as simple as that.

Well, of course it's not _that_ simple. We can start from the arguably more natural rules of the Clifford algebra, and discover that quaternions appear twice as Clifford algebras: the algebra of the negative-definite Euclidean plane \(\mathbb H \cong \operatorname{Cl}(\mathbb R^{0,2})\), and the even subalgebra of the algebra of the regular 3D space: \(\mathbb H \cong \operatorname{Cl}^0(\mathbb R^3)\). The latter is what actually connects quaternions with 3D rotations, while the former is just an instance of an infinite sequence of stupid coincidences of the form \(\operatorname{Cl}^0(\mathbb R^p) \cong \operatorname{Cl}(\mathbb R^{0,p-1})\).

Associativity

To this point I've somewhat ignored one other property of quaternion multiplication: associativity. It means simply that

\[ p\cdot(q\cdot r) = (p\cdot q)\cdot r \]

Or, put differently, it means that in a product of many quaternions like \(p\cdot q\cdot r\) you can place parentheses any way you want. In fact, without associativity the expression \(p\cdot q\cdot r\) doesn't even mean anything, because we've only defined multiplication of two quaternions! Again, this is an incredibly strong and useful rule that we're using all the time when doing computations with regular real numbers, and we're going to use it a lot with quaternions as well.

Now, is it a new rule, or does it follow from the definition of quaternions? Actually, it's the latter. We could pick up a multiplication table such that associativity doesn't hold! In fact, when proving that \(i^2=j^2=k^2=1\) leads to a contradiction, I implicitly assumed associativity. We could instead say that this rule doesn't lead to a contradiction, but simply isn't associative.

Specifically for the multiplication rules of quaternions, though, associativity does turn out to be true. You can check it by picking three arbitrary quaternions and multiplying them out in two different ways, — \((p\cdot q)\cdot r\) and \(p\cdot(q\cdot r)\), — and convincing yourself that the results are the same. This is a rather tedious task, so I won't be doing that computation here.

Mathematicians rarely work with operations that are not associative, simply because they are much more complicated to analyse. For example, usual composition of functions is associative, and mapping arbitrary objects to functions is a big part of algebra as a whole.

Quaternions: recap

I've said a lot of words, and by this time you might be completely lost. That's fine, it's a natural feeling when you're learning something new: at some point your brain just says "nope, that's enough, I'm outta here". Grab some tea or go for a walk; when you return, let's recap what we've learned:

Scalar-vector representation

We're now ready to do some explicit computations with quaternions: we know that quaternions are represented by packs of 4 numbers, and we know how to add and multiply these packs. However, this 4-number representation turns out to be a bit inconvenient compared another one.

Given a quaternion \(q = a+xi+yj+zk\), we usually call \(a\) the scalar part of the quaternion, while the 3D vector \(u=(x,y,z)\) is called the vector part of the quaternion. This way, we can represent a quaternion as a pair \((a,u)\) of a real number and a 3D vector. Or, introducing even more abuse of notation, we could write just \(a + u\), pretending that adding numbers to vectors makes sense (well, we've just defined it: the result is a quaternion). This might feel a bit crazy, but it also makes formulas much less scary. So, by the expression \(a+u\) I will mean the quaternion with scalar part \(a\) and vector part \(u\).

In this representation, quaternions \(i,j,k\) correspond to 3D vectors \((1,0,0)\), \((0,1,0)\) and \((0,0,1)\), — the usual coordinate axes of the 3D space.

Why is this representation useful? Well, if we take two quaternions in this scalar-vector form \(a+u\) and \(b+v\), plug them into the product formula, and gather the scalar and vector parts of the result separately, it turns out that the product can be expressed using some familiar operations from vector algebra:

\[ (a+u)\cdot (b+v) = (ab-\langle u,v \rangle) + (av+bu+u\times v) \]

Here, \(\langle u,v \rangle\) is the usual 3D dot product of vectors \(u\) and \(v\), while \(u \times v\) is the cross product of these vectors. So, the scalar part of the result \(ab-\langle u,v \rangle\) contains a product of numbers \(ab\) and a dot product of vectors \(\langle u,v \rangle\), while the vector part is two products of numbers and vectors \(av+bu\) and a cross product \(u\times v\).

Thus, we can reduce operations on quaternions to already familiar operations on the 3D vectors, which will simplify things a lot.

Oh, and, I didn't mention it, but adding quaternions in this representation also works coordinate-wise: \((a+u)+(b+v) = (a+b)+(u+v)\), the quaternion with scalar part \(a+b\) and vector part \(u+v\). As before, quaternions with zero vector part behave exactly like real numbers!

Conjugate and length

With this scalar-vector representation, we can finally do some explicit computations with quaternions. First, let's compute the square \(q^2\) of a quaternion \(q=a+u\), just for fun:

\[ q^2 = (a+u)\cdot(a+u) = (a^2-\langle u,u \rangle) + (au+au+u\times u) = (a^2-\langle u,u \rangle) + 2au \]

Here, we used the fact that \(u\times u=0\) for any 3D vector \(u\). Notice that if we change the sign of the vector part of one of the terms in the product, some terms will cancel, and we get

\[ (a+u)\cdot(a-u) = (a^2 - \langle u,-u\rangle) + (au-au+u\times(-u)) = (a^2+\langle u,u \rangle) + 0 \]

So, the product of \(a+u\) and \(a-u\) turns out to be a scalar quaternion (i.e. a number) \(a^2 + \langle u,u \rangle\): the square of the scalar part \(a^2\) plus the dot product of the vector part with itself \(\langle u,u \rangle\). You may recall from basic vector algebra that \(\langle u,u \rangle\) is just the squared length of the vector:

\[ \langle u,u \rangle = |u|^2 \]

If we spell out the coordinates of \(u=(x,y,z)\), and rewrite the quaternion using the full coordinates \(q = a+xi+yj+zk\), then the second term would be \(a-u = a-xi-yj-zk\), and the product above will be

\[ (a+xi+yj+zk)\cdot(a-xi-yj-zk) = a^2+|u|^2 = a^2+x^2+y^2+z^2 \]

which, if you look closely, is the usual Euclidean length of the 4D vector \((a,x,y,z)\), squared! We call the square root \(\sqrt{a^2+x^2+y^2+z^2}\) of this thing the length \(|q|\) of the quaternion \(q=a+u=a+xi+yj+zk\), and we call the second term \(q^*=a-u=a-xi-yj-zk\) the conjugate of \(q\).

So, we have two new definitions: for a quaternion \(q=a+u=a+xi+yj+zk\),

and the length can be computed through multiplication with the conjugate:

\[ |q|^2 = q\cdot q^* \]

By the way, the conjugate is also commonly denoted as \(\bar q\), but I think \(q^*\) looks a bit less noisy in complicated formulas.

Since negating the vector part of a quaternion twice gives us the original quaternion, it means that the conjugate of the conjugate is the original quaternion:

\[ (q^*)^* = q \]

and if we apply the length formula above to \(q^*\), we get

\[ |q^*|^2 = q^*\cdot (q^*)^* = q^*\cdot q \]

If we look closely at the length of the conjugate \(|q^*|^2\), we get

\[ |q^*|^2 = a^2 + \langle -u,-u \rangle = a^2 + (-x)^2 + (-y)^2 + (-z)^2 = \\ = a^2+x^2+y^2+z^2 = a^2 + \langle u,u \rangle = |q|^2 \]

So, a quaternion \(q\) has the same length as its conjugate \(q^*\)! Combining this with the formulas above, we get

\[ q\cdot q^* = |q|^2 = |q^*|^2 = q^*\cdot q \]

which means that the product of \(q\) with its conjugate in any order gives us the length of \(q\), which is the same as the length of \(q^*\). This is important, because it means that \(q\) and \(q^*\) commute: their product doesn't depend on the multiplication order, and we can swap this order in formulas if we need to.

Actually, we could prove that they commute \(q\cdot q^*=q^*\cdot q\) directly from the multiplication formula, but I figured it would be nice to see another way of proving it.

Conjugate and length of a product

A natural and useful question is: what happens if we take the conjugate of a product of two quaternions \(p\cdot q\)? We can, of course, plug it directly into the multiplication formula, but that's again a bit tedious. There's a simpler approach: let's guess what the result would be!

The simplest guess would be that \((p\cdot q)^* = p^*\cdot q^*\). To check if it's true, simply substitute \(p=i\) and \(q=j\):

\[ (i\cdot j)^* = k^* = -k\\ i^*\cdot j^* = (-i)\cdot(-j) = (-1)^2i\cdot j = i\cdot j = k\\ -k \, {\color{red}\neq} \, k \]

So, this is not the right formula. Maybe the answer is \((p\cdot q)^* = - p^*\cdot q^*\)? Substitute \(p=q=i\):

\[ (i\cdot i)^* = (-1)^* = -1 \\ -i^*\cdot i^* = -(-i)\cdot (-i) = - i\cdot i = -(-1) = 1\\ -1 \, {\color{red}\neq} \, 1 \]

Ok, that doesn't work either. Now, remember that quaternions are not commutative, and chaning the order of multiplication matters. Maybe we need to change the order?

\[ (p\cdot q)^* = q^* \cdot p^* \]

And indeed this is the correct formula! We can check that it works for all 16 pairs of basis quaternions \(1,i,j,k\), which would mean that it works for any quaternions.

For a generic product of a bunch of quaternions, this means that the conjugate of the product is the product of conjugates in the reversed order:

\[ (p_1\cdot p_2\cdot\dots\cdot p_n)^* = p_n^*\cdot\dots\cdot p_2^* \cdot p_1^* \]

From here, we can compute the length of the product of two quaternions:

\[ |p\cdot q|^2 = (p\cdot q)\cdot (p\cdot q)^* = (p\cdot q)\cdot(q^*\cdot p^*) = \\ = p\cdot (q\cdot q^*)\cdot p^* = p\cdot |q|^2 \cdot p^* = |q|^2 p\cdot p^* = |q|^2 |p|^2 \]

So, the length of a product is just the product of lengths, meaning that the length is multiplicative. This is an incredibly rare case in algebra! For example, the usual norms used for matrices are only sub-multiplicative: \(|A\cdot B| \leq |A|\cdot |B|\).

And again, this works for the product of any number of quaternions:

\[ |p_1\cdot\dots\cdot p_n| = |p_1|\cdot\dots\cdot|p_n| \]

Inverse and division

Given a quaternion \(q\), we call its inverse any quaternion \(p\) such that \(q\cdot p = 1\). Or, wait a minute, shouldn't we take the product in the other order: \(p\cdot q=1\)?

Luckily, it doesn't matter in our case, for two reasons:

  1. Quaternions are finite-dimensional (4-dimensional, to be specific), and it is a general fact that inverses are unique in finite dimensions (the proof is essentially the same as in my post about matrices)
  2. We've essentially already almost computed the inverse directly!

Look at the relation between conjugate and length once again:

\[ q\cdot q^* = q^*\cdot q = |q|^2 \]

Now, \(|q|^2\) is just a real number, so we can divide both sides by it (or multiply by its inverse — we already know what an inverse of a number is!):

\[ \frac{q\cdot q^*}{|q|^2} = 1 \]

Now, \(\frac{1}{|q|^2}\) is also just a number, and we can move it around however we like (remember, numbers commute with any quaternion!):

\[ q \cdot \frac{q^*}{|q|^2} = 1 \]

which means that \(\frac{q^*}{|q|^2}\) is the inverse \(q^{-1}\) of \(q\)! But what happens if we multiply them in a different order? Well, we already know that \(q\) and \(q^*\) commute, i.e. they don't care about the order we multiply them, and scaling one of them by a number \(\frac{1}{|q|^2}\) doesn't change that:

\[ \frac{q^*}{|q|^2}\cdot q = \frac{q^*\cdot q}{|q|^2} = \frac{|q|^2}{|q|^2} = 1 \]

In general, when talking about non-commutative stuff, we have to differentiate between left and right inverses. However, for quaternions things are simpler: we have a unique inverse \(q^{-1}\), and we even know a generic formula for it:

\[ q^{-1} = \frac{q^*}{|q|^2} = \frac{a-xi-yj-zk}{a^2+x^2+y^2+z^2} \]

The only way this formula can fail is when \(|q|^2=a^2+x^2+y^2+z^2=0\), but the length of a vector can be zero only if the vector itself is zero (i.e. a sum of squares is zero only if each term is zero). So, the only quaternion which can't be invered is the zero quaternion \(0+0i+0j+0k\), which is pretty much expected (if zero was invertible, we could quickly arrive at contradictions like \(0=1\)).

Now, what does it mean to divide one quaternion by another quaternion? Here's the sad story: it doesn't mean anything, i.e. it doesn't make sense, again, because multiplication is not commutative. Given quaternions \(p\) and \(q\), we simply cannot write something like \(\frac{p}{q}\). What we can do, though, it multiply be the inverse! But multiplication is not commutative, so we can multiply from two sides and get different results:

\[ p\cdot q^{-1} \neq q^{-1} \cdot p \]

In essense, division is the solution to an equation \(q\cdot x = p\). But in the non-commutative setting, this equation is different from \(x\cdot q=p\)! So we get two different equations with two different solutions:

\[ q\cdot x = p \Longrightarrow x = q^{-1}\cdot p \\ x\cdot q = p \Longrightarrow x = p\cdot q^{-1} \]

Let's repeat the important bits:

Note that for scalar quaternions \(q=a+0i+0j+0k\) (which behave like numbers) the inverse turns out to be the usual inverse

\[ (a+0i+0j+0k)^{-1} = \frac{a}{|a|^2} = \frac{1}{a} \]

and in this case it makes sense to divide by such a quaternion (again, because the inverse commutes with everything).

Unit quaternions

Notice that if the length of a quaternion is \(|q|=1\), then the formula for the inverse simplifies to

\[ q^{-1} = \frac{q^*}{|q|^2} = \frac{q^*}{1} = q^* \]

We call such quaternions unit quaternions, and for them inversion and conjugation are the same thing. Note that since the quaternion and its conjugate have the same length \(|q|=|q^*|\), if \(q\) is a unit quaternion, then so it \(q^*\).

Also, since the length of a product of quaternions is the same as product of lengths, it means that unit quaternions are closed under multiplication:

\[ |p|=|q|=1 \, \Longrightarrow |p\cdot q| = |p|\cdot|q|=1\cdot 1=1 \]

Finally, notice that the number \(1\) is also a unit quaternion. Together this means that unit quaternions form a group. This group is usually called the Spin(3) group.

Geometrically, unit quaternions are just 4-dimensional vectors \(p=(a,b,c,d)\) with the property that

\[ |p|^2 = a^2+b^2+c^2+d^2 = 1 \]

which is the equation of a hypersphere (namely, the 3-sphere inside the 4-dimensional space). I know, it can be rather hard to picture a sphere in 4 dimensions inside your head, but just think of it as the usual sphere in 3 dimensions, just somehow having one more extra dimension :) The point is that unit quaternions form some really nice, smooth, and highly symmetric thing.


Everyone does it.

Scalar and vector part via conjugation

Taking the conjugate of a quaternion allows us to extract the scalar and vector parts of a quaternion \(q=a+u\):

\[ q+q^* = (a+u) + (a-u) = 2a \\ q-q^* = (a+u) - (a-u) = 2u \]

So, the scalar part of a quaternion is \(\frac{q+q^*}{2}\), while the vector part is \(\frac{q-q^*}{2}\).

Likewise, we can check if a quaternion is purely a scalar, if its vector part is zero:

\[ q-q^*=0 \Longleftrightarrow q^*=q \]

and similarly a quaternion is purely a vector if its scalar part is zero:

\[ q+q^*=0 \Longleftrightarrow q^*=-q \]

Let's repeat that:

This will be useful for detecting when something is a vector later.

Since for purely vector quaternions \(v^*=-v\), we get

\[ v^2 = - v\cdot (-v) = -v\cdot v^* = -|v|^2 \]

So, the square of a vector quaternion is minus its squared length.

Yet again you might wonder: wouldn't it be nicer if the minus sign wasn't there? What if we tried to make a product rule such that the square of a vector is simply its squared length \(v^2=|v|^2\)? Indeed, we can do this! This is precisely the definition of Clifford algebra (aka geometric algebra), which is arguably a much more complicated thing to learn compared to purely quaternions.

Dot product via conjugation

Now, let \(p=a+u=(a,b,c,d)\) and \(q=w+v=(w,x,y,z)\) be two quaternions. Let's compute the product \(p\cdot q^*\):

\[ p\cdot q^* = (a+u)\cdot(w-v) = (aw+\langle u, v\rangle) + (-av+wu-u\times v) \]

Look at the scalar part of the result:

\[ aw+\langle u,v\rangle = aw+bx+cy+dz \]

It is just the dot product of \(p\) and \(q\) as 4-dimensional vectors! We will denote this as \(\langle p,q \rangle\). Now, we know how to extract the scalar part of the quaternion:

\[ \langle p,q \rangle = \frac{1}{2}\left(p\cdot q^* + (p\cdot q^*)^*\right) = \frac{1}{2}\left(p\cdot q^* + q\cdot p^*\right) \]

This formula gives us a way to compute the dot product between 4D vectors using just quaternion algebra! Notice that if \(p=0+u\) and \(q=0+v\) are vector quaternions, we have \(v^*=-v\) and \(u^*=-u\), and thus this simplifies to

\[ bx+cy+dz = \langle v,u \rangle = \frac{1}{2}\left(v\cdot (-u) + u\cdot (-v)\right) = -\frac{1}{2}\left(v\cdot u + u\cdot v\right) \]

Cross product via conjugation

You might've guessed that we can do a similar thing to extract the cross product of 3D vectors from the quaternion multiplication. Again, let \(p=v\) and \(q=u\) be vector quaternions (i.e. with scalar part being zero). Their product in general is

\[ v\cdot u = (-\langle v, u\rangle) + (v \times u) \]

So, the scalar part is minus the dot product \(-\langle v, u\rangle\), and the vector part is the cross product \(v\times u\). We know how to extract the vector part of a quaternion, so let's do that:

\[ v\times u = \frac{1}{2}\left(v\cdot u - (v\cdot u)^*\right) = \frac{1}{2}\left(v\cdot u - u^*\cdot v^*\right) = \\ = \frac{1}{2}\left(v\cdot u - (-u)\cdot (-v)\right) = \frac{1}{2}\left(v\cdot u - u\cdot v\right) \]

Operations: recap

Let's recap once again what we've learned so far:

Towards rotations

Unfortunately, this is the part when I'm forced to introduce another magic formula. It isn't obvious, it doesn't really come from anywhere, it just so happens that it works.

Let \(q\) be any quaternion, and let \(v\) be a purely vector quaternion, i.e. with scalar part equal to zero (and thus \(v^*=-v\)). We can think of \(v\) as simply a 3D vector embedded into the space of quaternions. Consider the formula

\[ q\cdot v\cdot q^* \]

Here's an important fact: \(u = q\cdot v\cdot q^*\) is also a purely vector quaternion. Let's prove this fact! For that, we need to check that \(u^*=-u\). Compute:

\[ u^* = (q\cdot v\cdot q^*)^* = (q^*)^*\cdot v^*\cdot q^* = q\cdot (-v)\cdot q^* = -q\cdot v\cdot q^*=-u \]

Hooray, \(u^*=-u\) means precisely that \(u\) is a vector quaternion. What is its length?

\[ |u| = |q|\cdot|v|\cdot|q^*| = |q|\cdot|v|\cdot|q| = |q|^2\cdot|v| \]

So, if \(q\) is a unit quaternion, i.e. if \(|q|=1\), then \(|u|=|v|\), meaning that the operation \(v\mapsto qvq^*\) preserves lengths!

Maybe it even preserves arbitrary dot products? Say, we have two vector quaternions \(u\) and \(v\), and we apply the operation to both of them, and compute the dot product, what will it be? Well, we already know how to extract the dot product of 3D vectors using just quaternion algebra, so let's put everything together:

\[ \langle pvp^*, pup^* \rangle = -\frac{1}{2}\left((pvp^*)\cdot(pup^*)+(pup^*)\cdot(pvp^*)\right) = -\frac{1}{2}\left(pv(p^*p)up^* + pu(p^*p)vp^*\right) = \\ = -\frac{1}{2}\left(pv\cdot |q|^2\cdot up^* + pu\cdot |q|^2 \cdot vp^*\right) = -\frac{1}{2}\left(pvup^*+puvp^*\right) = -\frac{1}{2}\left(p(vu)p^*+p(uv)p^*\right) = \\ = -p\frac{1}{2}\left(vu + uv\right)p^* = p\cdot\langle v,u\rangle\cdot p^* = \langle v,u\rangle\cdot p\cdot p^* = \langle v,u\rangle \cdot |p|^2 = \langle v,u\rangle \]

That's a rather long derivation, but it only uses the very basic formulas we've derived earlier, and doesn't contain any special tricks.

So, the operation \(v\mapsto qvq^*\) preserves arbitrary dot products! This means it preserves angles as well. This means that it is a rotation.

Well, actually, no, it could still be something like a reflection — they also preserve dot products, but reverse the orientation of the space.

We can check if \(v\mapsto qvq^*\) preserves or reverses orientation by applying to to the three basis vectors \(i,j,k\): the result would be 3 orthogonal unit vectors, but they might be a left or a right-handed triple. We can take the scalar triple product of them; if it is equal to \(1\), the operation preserves orientation, and if it is \(-1\), it reverses it. Alternatively, we take the cross product of the first two vectors \(pip^*\) and \(pjp^*\): it should be either \(pkp^*\) or \(-pkp^*\), depending on whether it the orientation is preserved or reversed. Here's the boring derivation:

\[ (pip^*)\times(pjp^*) = \frac{1}{2}(pip^*pjp^*-pjp^*pip^*) = \frac{1}{2}(pijp^*-pijp^*) = \\ = \frac{1}{2}(pkp^*-p(-k)p^*) = \frac{1}{2}(pkp^*+pkp^*)=pkp^* \]

Hooray, our operation preserved orientation, and also preserves dot products. That's it, that's literally the definition of a rotation! Let's spell it again:

Composing rotations

Say we have two unit quaternions \(p\) and \(q\), and we want to apply the rotation by \(q\), and then the rotation by \(p\), to some vector \(v\). This is relatively straightforward:

\[ p(qvq^*)p^* = (pq)v(q^*p^*) = (pq)v(pq)^* \]

So, the composition of rotations is the same as the rotation by the product quaternion \(pq\)! This is where the true power of quaternions lies: when combining many rotations, we can still represent the result as a quaternion, and we know the simple and explicit formula for computing the result (i.e. quaternion multiplication).

But can every rotation be represented by a quaternion?

Analyzing rotations

Say I have a unit quaternion \(p=a+v\), and I want to understand the rotation \(u\mapsto pup^*\) it represents. It might be helpful to apply this rotation to some specific vectors!

First, let's apply it to the vector \(v\), which is the vector part of the quaternion itself. Remember that \(a\) is a number, so it commutes with everything; \(v\) is a vector, but it commutes at least with itself (because \(v\cdot v=v\cdot v\) – changing order doesn't change anything). This means that \(v\) must commute with \(a+v\) and \(a-v\), and we have

\[ qvq^* = (a+v)v(a-v) = (a+v)(a-v)v = qq^*v = |q|^2v = v \]

So, the rotation by the quaternion \(a+v\) doesn't change the vector \(v\)! This means that \(v\) must be parallel to the rotation axis of our quaternion, and the rotation happens in the plane orthogonal to \(v\) (as long as \(v\neq 0\)).

Constructing specific rotations

To better understand what a specific rotation quaternion should look like, let's try to construct a rotation in the XY plane. We know that the vector part of the rotation quaternion must be parallel to the rotation axis, which in this case would be the Z axis, represented by the quaternion \(k\). So our XY-rotation quaternion looks like

\[ p = a+bk \]

with the constraint that

\[ |p|^2 = a^2+b^2 = 1 \]

Let's look explicitly what this rotation does to the X axis, i.e. to the \(i\) quaternion:

\[ pip^* = (a+bk)i(a-bk) = (ai+bki)(a-bk) = (ai+bj)(a-bk) =\\ = a^2i-abik+abj-b^2jk = a^2i+abj+abj-b^2i = (a^2-b^2)i+2abj \]

If you look at this and see the formula fot the square of a complex number, you're not wrong!

We know that a general rotation by an angle \(\theta\) should map the X axis to something like

\[ \cos\theta i + \sin\theta j \]

Thus, we have

\[ a^2-b^2 = \cos\theta \\ 2ab = \sin\theta \]

From here, we could refer to how rotations are realized by complex numbers, or to the formulas for \(\sin\) and \(\cos\) of double angles. In any case, we can deduce that

\[ a = \cos\frac{\theta}{2}\\ b = \sin\frac{\theta}{2} \]

and our rotation quaternion looks like

\[ p = \cos\frac{\theta}{2} + \sin\frac{\theta}{2}k \]

This is the rotation in the XY plane. What about a generic rotation?

Constructing generic rotations

We know from a theorem by Euler that any 3D rotation is a rotation by a certain angle \(\theta\) around a certain axis \(n\) (which we assume is a normalized vector). How can we represent such a rotation by a quaternion?

Here's where we employ the fact that unit quaternions form such a nice, symmetric thing. We've already proved that \(\cos\frac{\theta}{2} + \sin\frac{\theta}{2}k\) is a \(\theta\)-radian rotation in the XY plane. However, the axes in a space are really completely arbitrary. I could pick any unit vector and call it the Z axis, and find any two other unit vectors orthogonal to Z and to each other, and call them X and Y axes. A particular choice of coordinates shouldn't matter!

This means that the same formula should work for a rotation around an arbitrary axis: just replace \(k\) with \(n\):

\[ p = \cos\frac{\theta}{2} + \sin\frac{\theta}{2}n \]

This is the unit quaternion that represents a rotation by an angle of \(\theta\) around the axis \(n\)!

There are several ways of proving this. One simple way is to pick a basis for the plane orthogonal to \(n\) and explicitly compute what this rotation looks like in this basis. We should end up with formulas similar to those in the previous section, and get something like \(\cos^2{\theta\over 2} - \sin^2{\theta\over 2}=\cos\theta\), etc, which will mean that it is indeed a rotation by an angle \(\theta\).

Let's repeat this once again, because it might be the most important formula here:

In reverse, given a quaternion \(p=a+v\), we can readily extract the axis and angle: the axis is \(n=\frac{v}{|v|}\) and the angle is \(\theta=2\arccos a\).

You might think: wait, what if there is no axis of rotation? What if it is the identity rotation, i.e. a rotation by \(0^\circ\)? Actually, everything works just fine! A rotation by \(0^\circ\) is the same around any axis (because it doesn't do anything), so we can pick any unit vector \(n\) and compute the quaternion:

\[ p = \cos 0 + \sin 0 \cdot n = 1 + 0 \cdot n = 1 \]

Thus, the resulting quaternion is just the quaternion \(p=1\), or in full coordinates \(1 + 0i + 0j + 0k\).

Relation between rotations and unit quaternions

You might think: what about a \(360^\circ\) rotation? It should still be an identity operation (nothing changes if you rotate full circle!), so it should also be represented by the same quaternion \(p=1\)? Let's check:

\[ p = \cos{360^\circ\over 2} + \sin{360^\circ\over 2}\cdot n = \cos 180^\circ + \sin 180^\circ\cdot n = -1 + 0\cdot n = -1 \]

Thus, this rotation is represented by a different quaternion, but it must be the same rotation! What's going on?

Actually, nothing is wrong. We said that any rotation can be represented by a quaternion, but we din't say that this quaternion is unique! In fact, if \(p\) is a unit quaternion, then \(-p\) always represents the same rotation:

\[ (-p)v(-p)^* = (-1)^2 pvp^* = pvp^* \]

This corresponds to the fact that rotating by an angle \(\theta\) around an axis \(n\) is the same as rotating by an angle \(-\theta\) (i.e. rotating in the different direction) around the axis \(-n\). In other words, a clockwise rotation in a plane turns into a counterclockwise rotation when you look at it from the other side of the plane!

It turns out that there are no other quaternions other that \(\pm p\) that represent the same rotation. There are many ways to prove it; one particularly direct method is to take any two quaternions \(p,q\) and assume the \(pvp^*=qvq^*\) for any vector \(v\); then substitute \(v=i,j,k\), you'll get 3 equalities of 3D vectors, so 9 equations in total, which will be quadratic equations in the coordinates of \(p\) and \(q\). Solving the system should give only two possibilities: \(p=q\) or \(p=-q\).

So, let's restate this once again:

In topology, we say that unit quaternions form a double cover of the 3D rotations.

Some notes on the rotation formula \(pvp^*\)

First, why is there a \({\theta\over 2}\) in all the formulas? Why not just \(\theta\), if that's the angle of rotation? Well, one explanation could be that we're multiplying with the quaternion \(q\) twice: once on the left, once on the right. So, if both used \(\theta\) in the formulas, we'd get a total rotation of \(2\theta\) instead. But this argument feels a bit backwards: why do we multiply twice, then? Why not just multiply once, e.g. \(q\cdot v\)?

Roughly speaking, multiplying on just one side \(q\cdot v\) leaves some extra garbage that we don't need (that prevents the result from being a 3D vector rather than a generic 4D quaternion). Multiplying from both sides, one conjugated and one not, works out to cancel this extra garbage, and the result is a nice 3D vector. In order to compensate for this two-sided multiplication, we have to take half the angle in the formulas.

The formula itself can be traced to Clifford (aka geometric) algebra, where the formula \(v \mapsto -n\cdot v\cdot n\) implements a reflection through a hyperplane orthogonal to \(n\), and the Cartan–Dieudonné theorem says that any rotation can be realized as a composition of reflections. However, while it's not hard to check that \(-n\cdot v\cdot n\) is indeed a reflection, the formula itself doesn't naturally follow from anything else.

Another note: since for unit quaternions \(q^*=q^{-1}\), we could instead take the formula \(v \mapsto qvq^{-1}\). For unit quaternions there's no difference, but for general quaternions this is a different operation!

For non-unit quaternions, \(qvq^*\) is a rotation together with scaling by \(|q|^2\). However, \(qvq^{-1}\) is still just a rotation, because the lengths of \(q\) and \(q^{-1}\) cancel out. So, with the formula \(qvq^{-1}\), any non-zero multiple of \(q\) represents the same rotation, while with the formula \(qvq^*\) it is possible to incorporate scaling into quaternions as well.

Rotations: recap

Quaternions in Clifford (aka geometric) algebra

This section is rather advanced and assumes a bit of familiarity with geometric algebra.

The Clifford algebra of the 3D Euclidean space \(\operatorname{Cl}(\mathbb R^3)\) is defined by the following rules (which look a bit similar to quaternions!)

This last "no extra relations" property is tricky, but not impossible to formalize. Once again, category theory provides the tools to deal with such abstract stuff.

This algebra turns out to be \(2^3=8\)-dimensional, and it has a basis

\[ \{ 1, e_1, e_2, e_3, e_1e_2, e_1e_3, e_2e_3, e_1e_2e_3 \} \]

where \(\{e_1,e_2,e_3\}\) is the orthonormal basis of the 3D space itself. The multiplication table is

\[ e_1^2=e_2^2=e_3^2=1 \\ e_1e_2=-e_2e_1\\ e_1e_3=-e_3e_1\\ e_2e_3=-e_3e_2 \]

i.e. the basis vectors square to 1 and anti-commute with each other.

From here, it isn't hard to prove that e.g.

\[ (e_1e_2)^2 = e_1e_2e_1e_2 = e_1(e_2e_1)e_2 = -e_1(e_1e_2)e_2 = -e_1^2e_2^2 = -1 \]

and similarly for \(e_1e_3\) and \(e_2e_3\). Furthermore,

\[ (e_1e_2)\cdot(e_2e_3) = e_1(e_2e_2)e_3 = e_1e_3 \]

and etc. Defining \(i,j,k\) to be the bivectors

\[ i = e_3e_2 = -e_2e_3\\ j = e_1e_3 = -e_3e_1\\ k = e_2e_1 = -e_1e_2 \]

we get that the subspace of elements of the form \(a+bi+cj+dk\) is closed under multiplication and is isomorphic to quaternions. This is called the even subalgebra \(\operatorname{Cl}^0\) of the full Clifford algebra, because it only contains products of even number of vectors. Note that a vector is a product of an odd number of vectors (namely, a product containing 1 vector), so vectors don't belong to the even subalgebra.

The analogue of conjugation in a Clifford algebra is called the transpose and it simply reverses the order of vectors in a product:

\[ e_1^T = e_1\\ (e_1e_2)^T = e_2e_1 = -e_1e_2\\ (e_1e_2e_3)^T = e_3e_2e_1 = -e_1e_2e_3 \]

which leads to

\[ 1^T = 1\\ i^T = -i\\ j^T = -j\\ k^T = -k \]

i.e. on the even subalgebra transpose works exactly like quaternion conjugation.

Finally, given an element \(p\) which is a product of an even number of unit vectors (which will be a unit quaternion; in this context they are also called rotors), the formula for rotation looks like

\[ v \mapsto pvp^T \]

Since for quaternions aka the even subalgebra we have \(p^T=p^*\), it might seem that this is the same exact formula that we used for quaternions. However, this is a deceit: the identification of vectors and quaternions is different from the identification of vectors and elements of the Clifford algebra! Specifically, in the Clifford algebra the 3D vector \((x,y,z)\) maps to

\[ xe_1+ye_2+ze_3 \]

while in the quaternions it maps to

\[ xi+yj+zk = xe_3e_2+ye_1e_3+ze_2e_1 \]

This can be repaired using something called the unit pseudoscalar \(\omega=e_1e_2e_3\). Notice that

\[ \omega e_3 = e_1e_2e_3e_3 = e_1e_2 = -e_2e_1 \\ \omega e_2e_1 = e_1e_2e_3e_2e_1 = e_3 \]

and etc, so we can bridge the two rotation formulas together: given a vector in the quaternion representation \(v=xe_3e_2+ye_1e_3+ze_2e_1\), the element \(\omega\cdot v\) is a vector \(xe_1+ye_2+ze_3\) in the Clifford algebra representation, and we can apply the Clifford algebra rotation to it \(p\omega v p^T\), and then transform it back to the original quaternion representation by multiplying with \(-\omega\):

\[ v \mapsto -\omega p \omega v p^T \]

Finally, notice that

\[ \omega^2 = e_1e_2e_3e_1e_2e_3 = -1 \\ \omega e_2e_1 \omega = e_1e_2e_3e_2e_1e_1e_2e_3 = -e_2e_1 \]

and etc, meaning that if \(p\) is an element of the even subalgebra (aka a quaternion), then \(-\omega p \omega = p\), and the formula above simplifies to

\[ v \mapsto (-\omega p \omega) v p^T = pvp^T = pvp^* \]

which is indeed the original formula for the quaternion rotation, but this time all multiplications happen inside the 4-dimensional even subalgebra (aka quaternions) instead of the general 8-dimensional Clifford algebra.

Quaternions cheatsheet

Here's everything we've learnt today, organized in a single table:

Quaternion as a 4-tuple of real numbers \[ q=(a,b,c,d) \]
Basis quaternions \[ \mathbb I = (1,0,0,0) \\ i = (0,1,0,0) \\ j = (0,0,1,0) \\ k=(0,0,0,1) \]
Scalar quaternions that behave like real numbers \[ (a,0,0,0) = a\mathbb I = a \]
Quaternion as a sum of basis quaternions \[ q=a + bi+cj+dk \]
Quaternion as a scalar-vector pair \[ q=(a,u) = a + u \]
Basis quaternion multiplication rules \[ i^2=j^2=k^2=-1 \\ ij=-ji=k \\ jk=-kj=i \\ ki=-ik=j \]
Quaternion multiplication in the scalar-vector representation \[ (a,v) \cdot (b,u) = (ab-\langle v,u \rangle, au+bv+v\times u) \]
Quaternion conjugation \[ q^* = a-u = a-bi-cj-dk \\ (pq)^* = q^*p^* \]
Quaternion length \[ |q|^2 = a^2+|u|^2 = a^2+b^2+c^2+d^2 = q\cdot q^* \\ |pq| = |p|\cdot |q| \]
Quaternion inverse \[ q^{-1} = \frac{q^*}{|q|^2} \]
Unit quaternion \[ |q|=1 \\ q^* = q^{-1} \]
Scalar quaternion \[ q = a + 0 = (a,0,0,0) \\ q^*=q \]
Vector quaternion \[ u = 0 + u = (0,x,y,z) \\ q^*=-q \]
Quaternion scalar part \[ a = \frac{1}{2}(q+q^*) \]
Quaternion vector part \[ u = \frac{1}{2}(q-q^*) \]
Quaternion dot product \[ \langle p, q \rangle = \frac{1}{2}(pq^*+qp^*) \]
3D vector cross product \[ u \times v = \frac{1}{2}(uv^*+vu^*) = -\frac{1}{2}(uv+vu) \]
Rotation by unit quaternion \[ |q|=1 \\ v\,\mapsto\, qvq^* \]
Composition of rotations \[ p, q \Rightarrow pq \\ v\mapsto p(qvq^*)p^* = (pq)v(pq)^* \]
Inverse rotation \[ p \Rightarrow p^{-1} \]
Rotation by axis-angle \[ q = \cos\frac{\theta}{2} + \sin\frac{\theta}{2} \cdot n = \\ = \left(\cos\frac{\theta}{2}, \sin\frac{\theta}{2}\cdot n_x, \sin\frac{\theta}{2}\cdot n_y, \sin\frac{\theta}{2}\cdot n_z\right) \]

Other resources on quaternions

Check out these cool resources on quaternions as well:

I know that it was a ton of formulas and algebra, but hey, that's how I understand things, and I wanted to share it with you. I hoped you've learnt at least something useful! As always, thanks for reading.